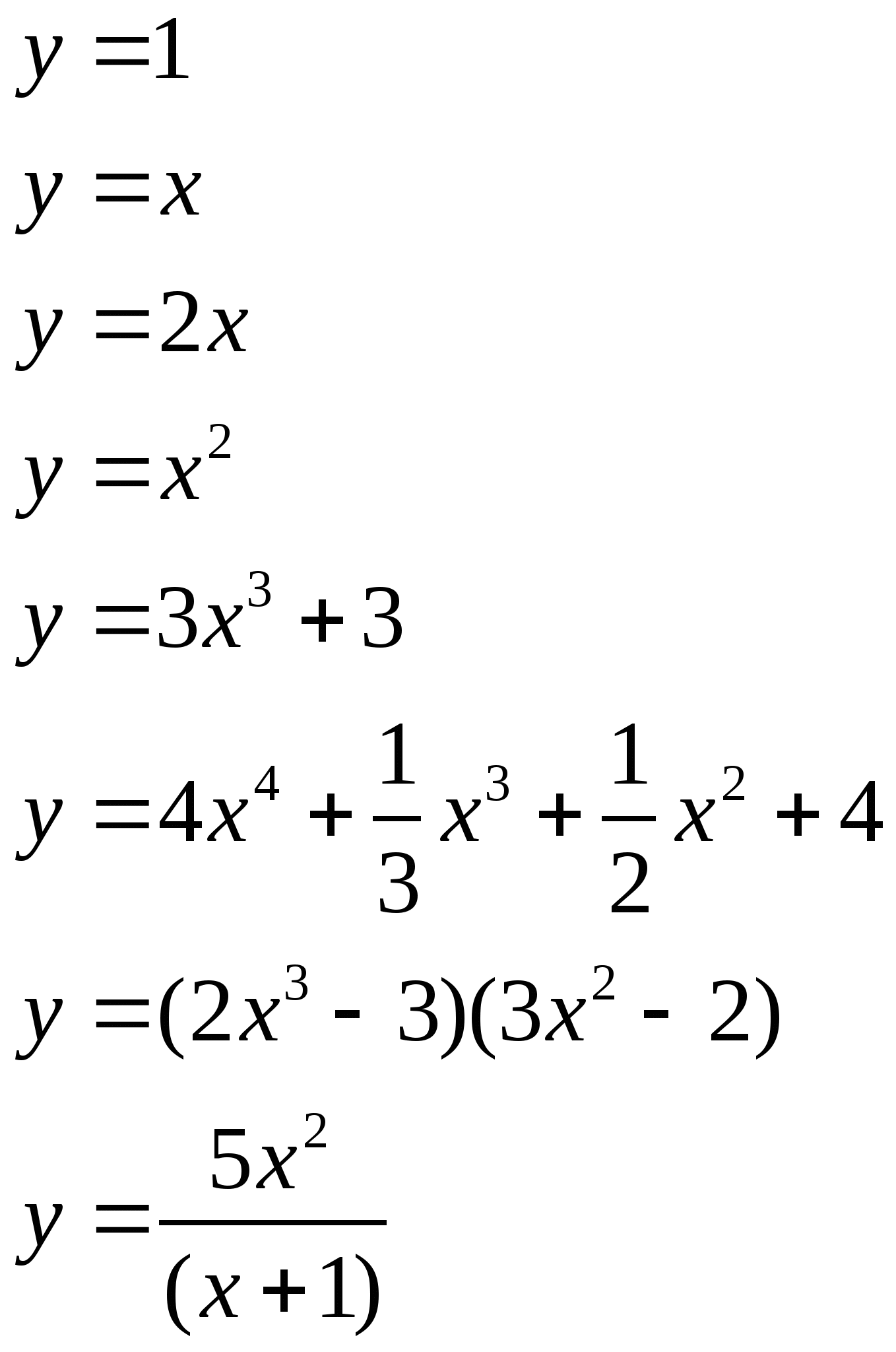Самостоятельная работа "Производные некоторых элементарных функций"
Используя определения, найдите производные и дифференциалы следующих функций:. Определите значение производной , если касательная, проведенная к графику функции в точке , пересекает координатные оси в точках и :. Ответы: 1 2 ; 3 4. К графику функции в точке проведена касательная, проходящая через точки Определите значение производной. К графику функции в точке проведена касательная, которая образует с положительным направлением оси абсцисс угол: 1 ; 2 ; 3 ; 4. Определите значение производной.

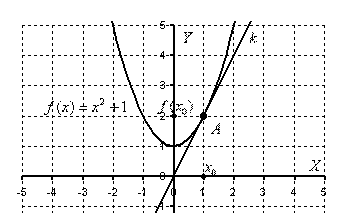








Серия задач 2. Найдите производную данной функции f x и вычислите ее значение в точке x 0 :. Серия задач 3.




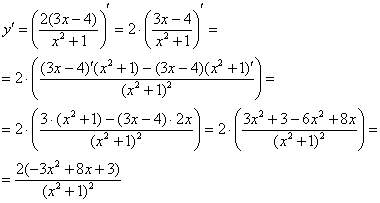
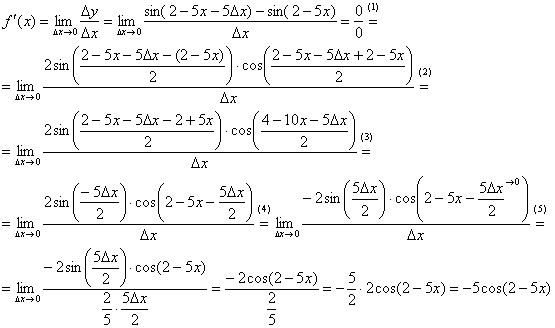







Категория: Математика. Похожие презентации:. Производная и дифференциал. Производные высших порядков.