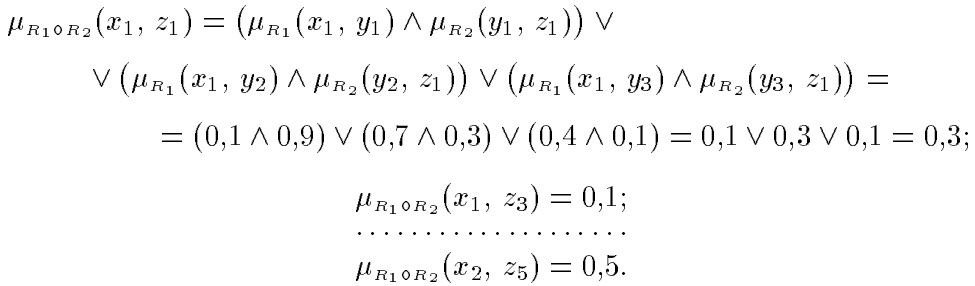
Часть 4. Нечеткие отношения
Нечеткие отношения играют фундаментальную роль в теории нечетких систем. Аппарат теории нечетких отношений используется при построении теории нечетких автоматов, при моделировании структуры сложных систем, при анализе процессов принятия решений. Теория нечетких отношений находит также приложение в задачах, в которых традиционно применяется теория обычных четких отношений. Как правило, аппарат теории четких отношений используется при качественном анализе взаимосвязей между объектами исследуемой системы, когда связи носят дихотомический характер и могут быть проинтерпретированы в терминах " связь присутствует", " связь отсутствует", либо когда методы количественного анализа взаимосвязей по каким-либо причинам неприменимы и взаимосвязи искусственно приводятся к дихотомическому виду. Например, когда величина связи между объектами принимает значения из ранговой шкалы, выбор порога на силу связи позволяет преобразовать связь к требуемому виду. Однако, подобный подход, позволяя проводить качественный анализ систем, приводит к потере информации о силе связей между объектами либо требует проведения вычислений при разных порогах на силу связей.
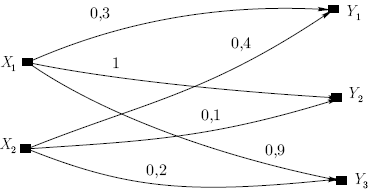
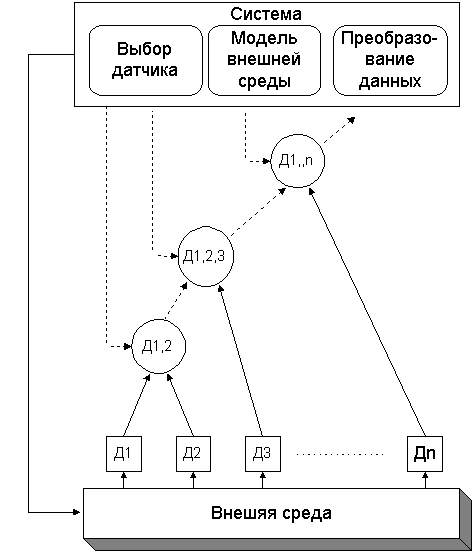
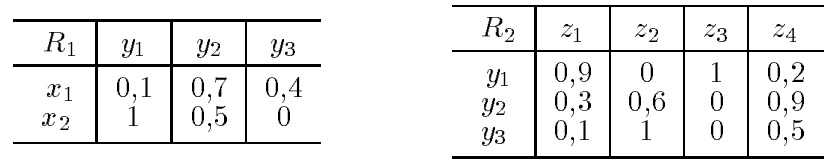

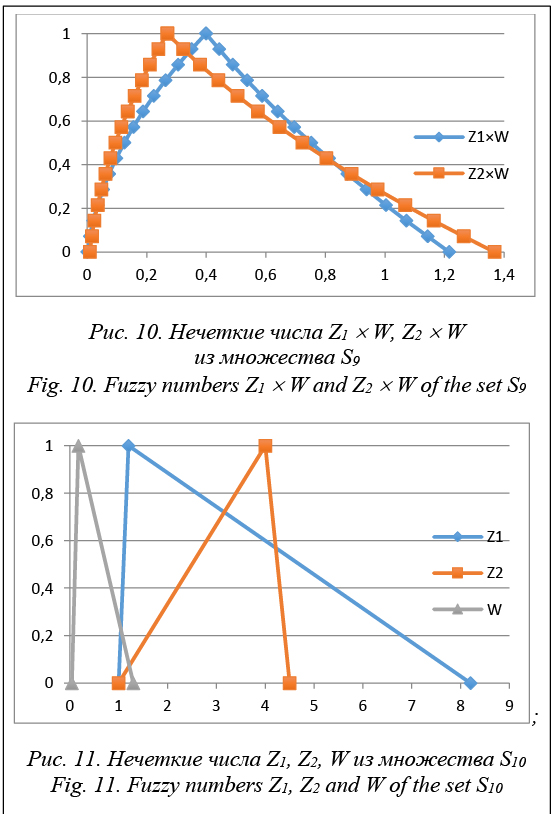
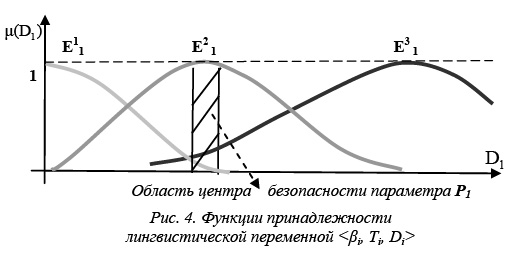




Ранее были сформулированы операции над нечеткими отношениями см. В результате изучения материалов текущей лекции предполагается, что Обучающийся узнает, как определяется композиция бинарных нечётких отношений, а также каковы её отличия от других бинарных операций над бинарными нечёткими отношениями. Напомним определение бинарного нечёткого отношения учитывая, что Обучающийся знаком с понятием декартового произведения :. Обратим ещё раз внимание на то, что первое из бинарных нечётких отношений задано на декартовом произведении универсальных множеств I 1 на I 2, а второе бинарное нечёткое отношение задано на декартовом произведении универсальных множеств I 2 на I 3,.
- 4.4 Свойства нечетких отношений
- В материале текущей лекции сформулируем ряд важных понятий, а также рассмотрим основные характеристики нечётких отношений.
- Нечеткое n-арное отношение определяется как нечеткое подмножество R на E , принимающее свои значения в М. Носителем нечеткого отношения R называется обычное множество упорядоченных пар x,y , для которых функция принадлежности положительна:.
- Поиск Настройки.
- Рекомендуемые материалы
- Прежде чем ввести понятие нечеткого отношения , рассмотрим обычные отношения и их свойства. Отношением на множестве называется некоторое подмножество декартова произведения.
- Декартово произведение нечетких множеств — это нечеткое множество всех возможных кортежей, составленных из элементов исходных множеств, функция принадлежности которых вычисляются по соотношениям: m x1, x2, Нечетким отношением называется нечеткое подмножество декартова произведения доменов, характеризующееся функцией принадлежности.
- Одним из основных понятий теории нечетких множеств считается понятие нечеткого отношения. Эти отношения позволяют формализовать неточные утверждения типа « почти равно » или « значительно больше чем ».
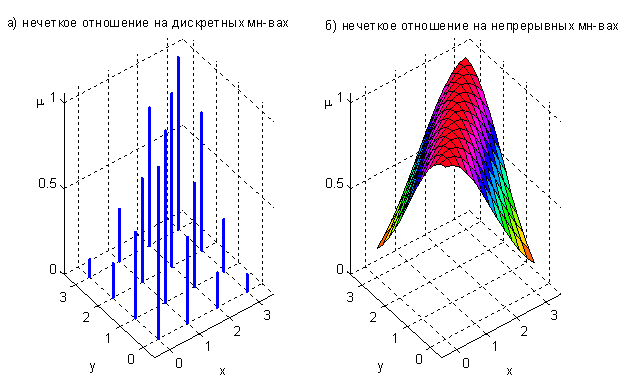
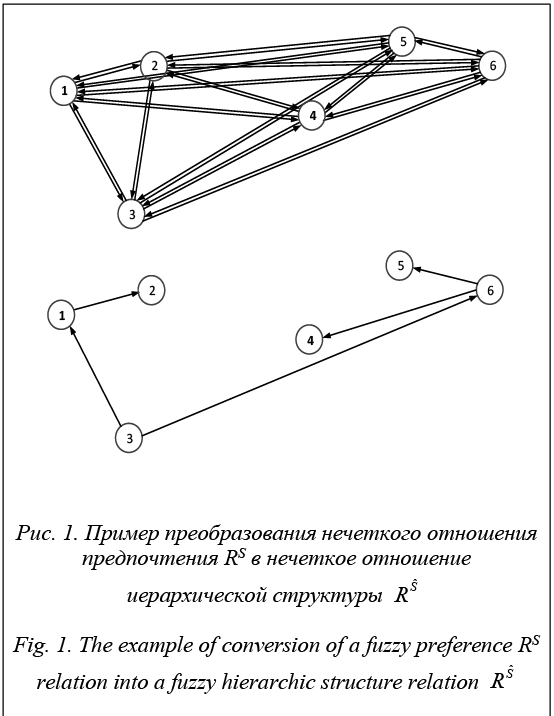

.jpg)

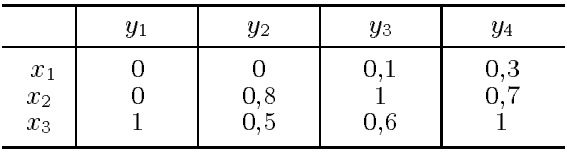

Для практических задач большое значение имеет понятие нечеткого отношения. Пусть имеется набор универсальных множеств. Возьмем прямое декартово произведение этих множеств и некоторое множество принадлежностей например, [0,1]. Тогда нечеткое -арное отношение определяется как нечеткое подмножество на , принимающее свои значения в [0,1].