Что такое синус, косинус, тангенс, котангенс
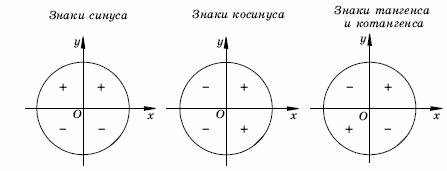
Синус угла обозначается — ордината точки полученной поворотом точки вокруг начала координат на угол. Косинус угла обозначается — абсцисса точки полученной поворотом точки вокруг начала координат на угол. Тангенс угла обозначается — отношение синуса угла к его косинусу, то есть. Котангенс угла обозначается — отношение косинуса угла к его синусу, то есть.
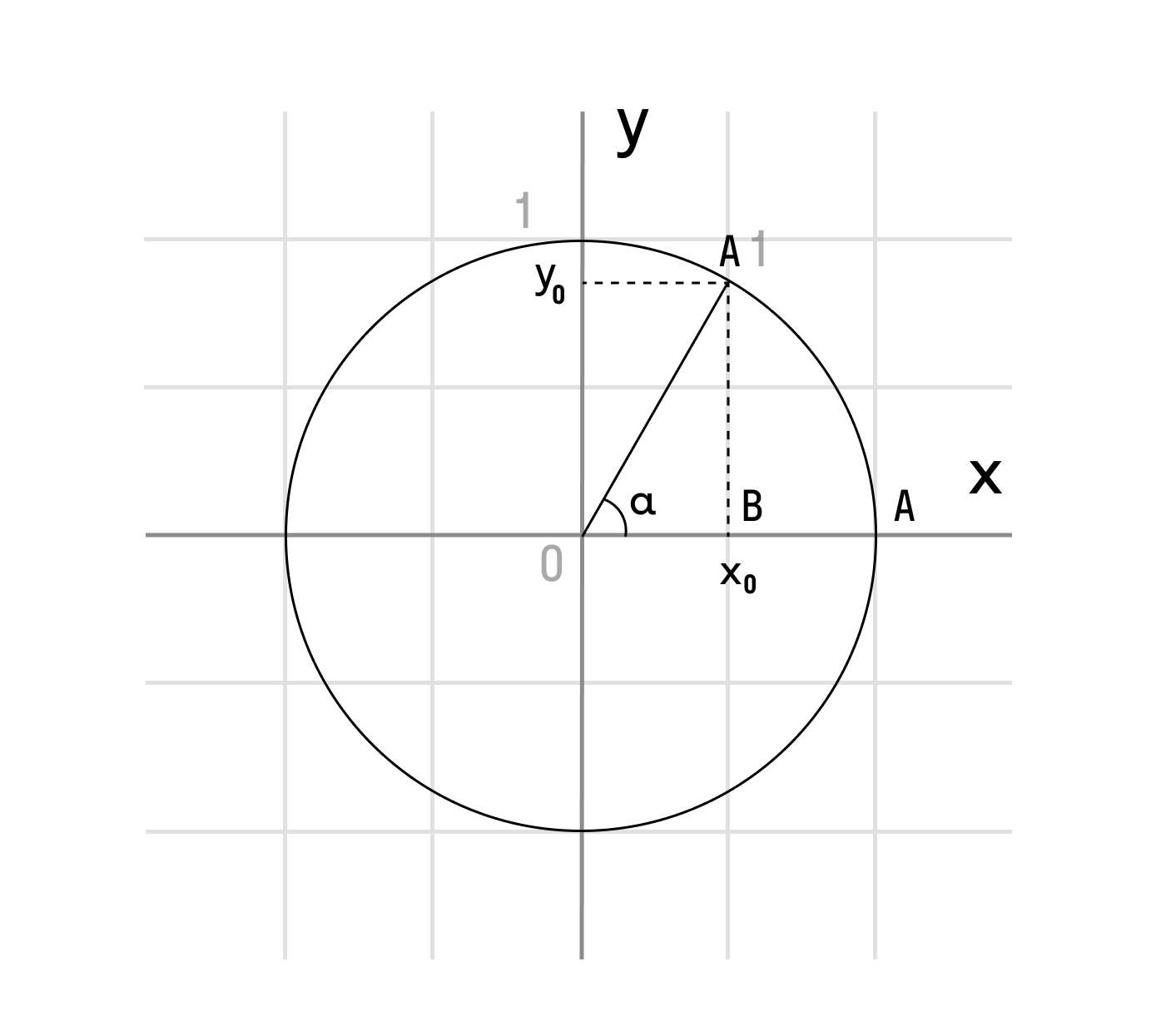

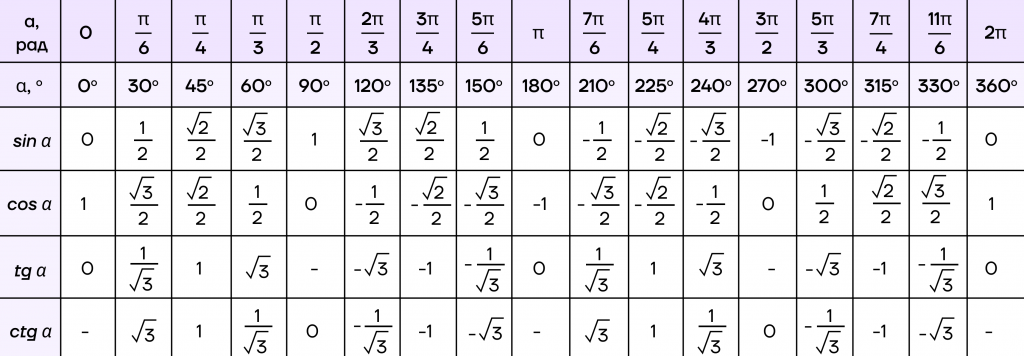
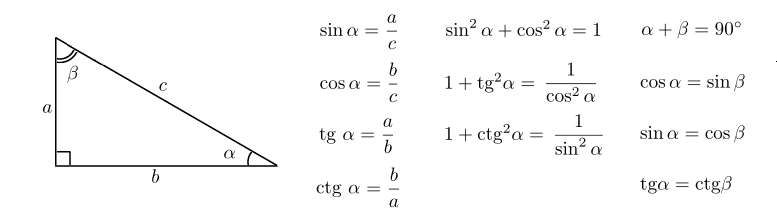



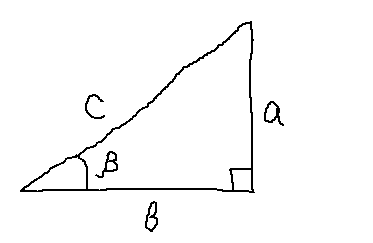
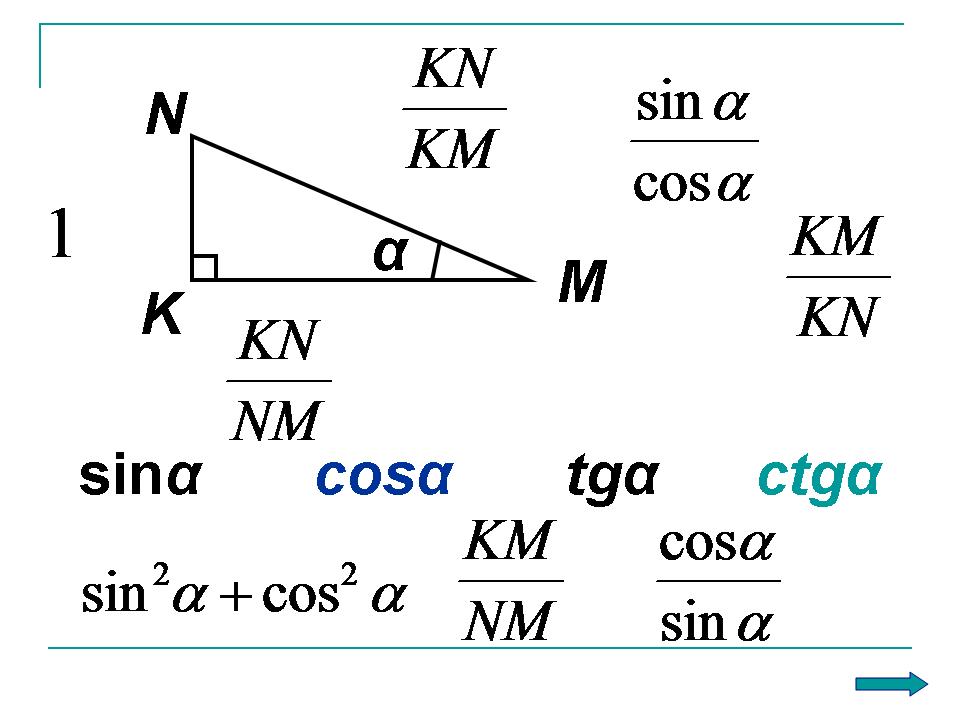
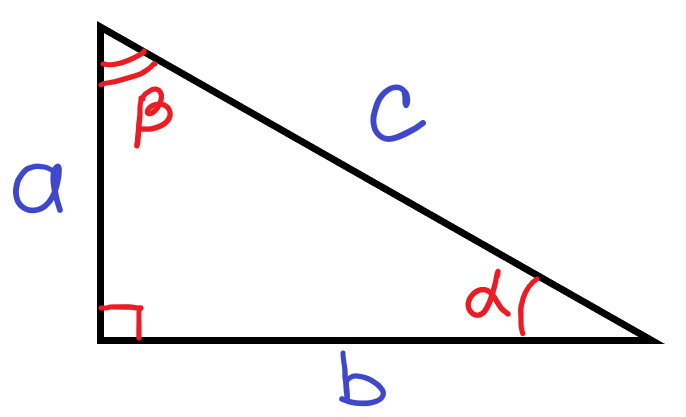
Чтобы хорошо разобраться в этих понятиях нет, не в чёрте! Синус угла — это отношение противолежащего дальнего катета к гипотенузе. Косинус угла — это отношение прилежащего близкого катета к гипотенузе.
- Бесплатные вебинары
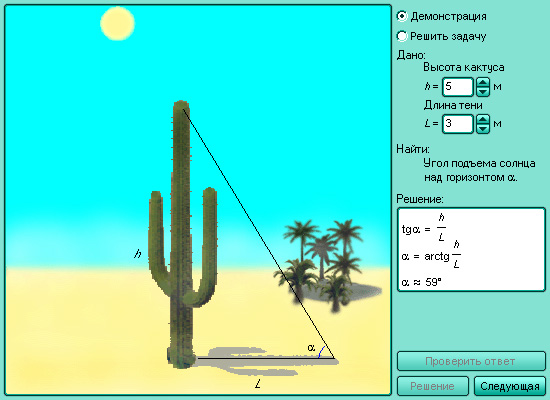
- Эти функции нашли широкое применение в самых разных областях науки.
- Вход Регистрация. Учебные заведения.
- В данном материале, мы изучим основное определение тригонометрии , какие свойства ей характерны, применение в математике, приведем примеры решения уравнений.
- Теорема синусов в формуле:
- Из свойств подобных треугольников следует, что синус, косинус, тангенс и котангенс не зависят от размеров треугольника, а однозначно определяются углом ,.
- Там, где заканчиваются границы привычной и давно знакомой алгебры, начинаются владения тригонометрии.
- Сегодня мы узнаем, что такое синус, косинус, тангенс и котангенс. Это первый и самый важный урок по тригонометрии на всём сайте.
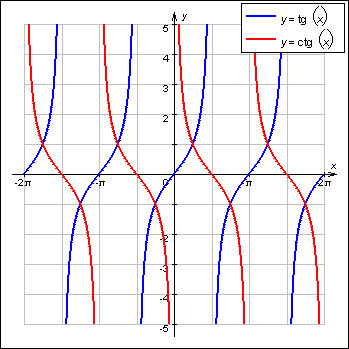
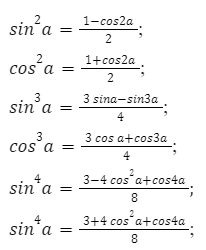

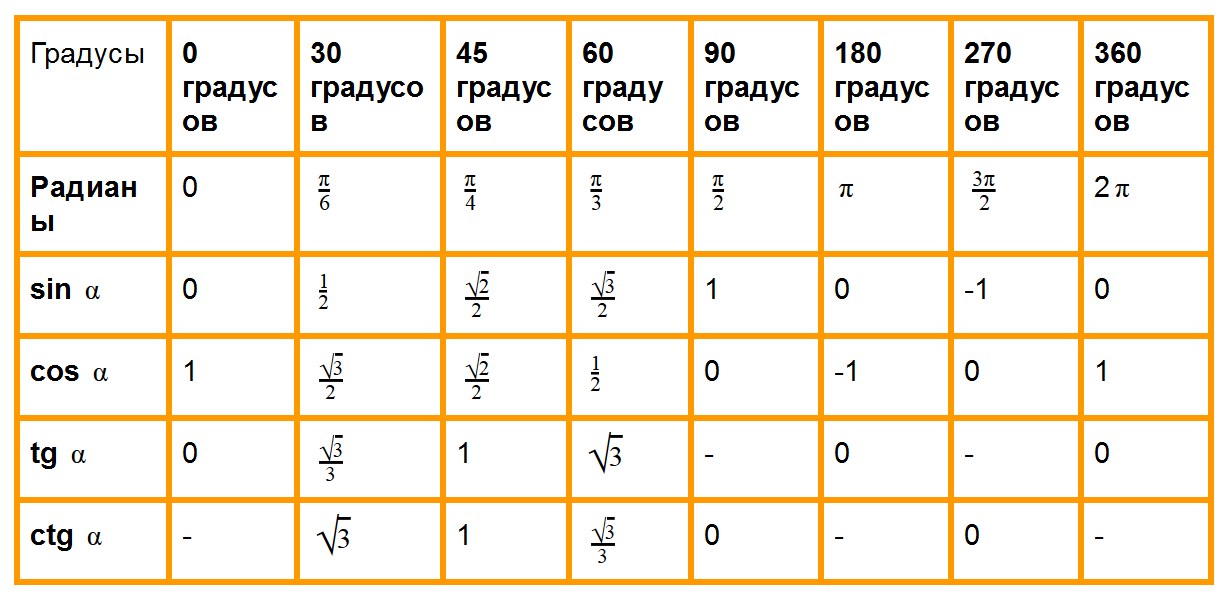
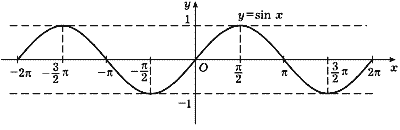


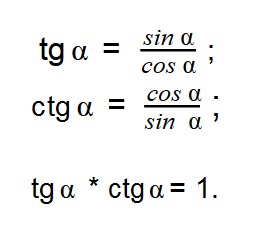


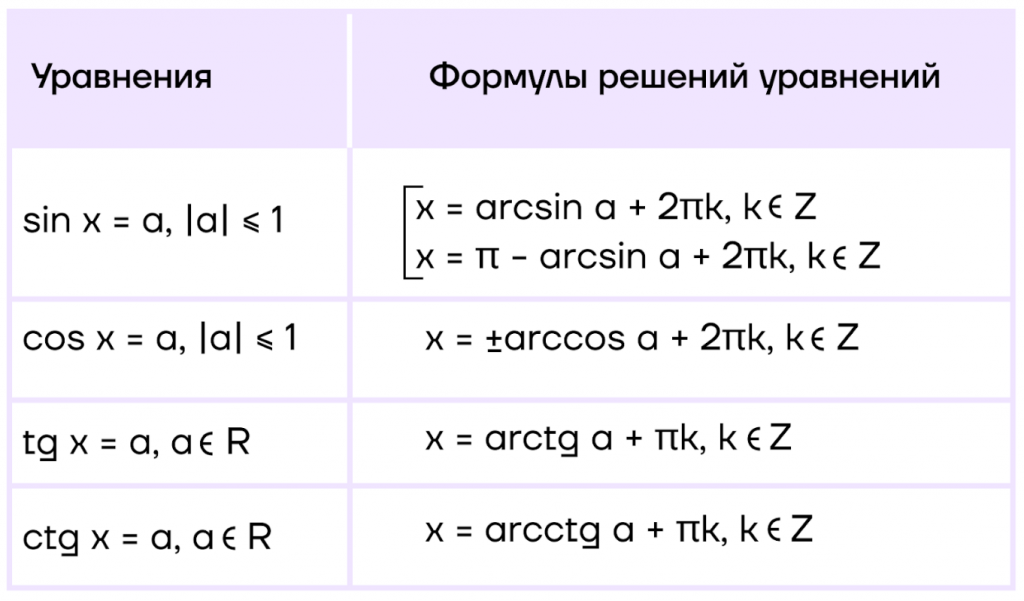
Итак, в прошлый раз мы с вами успешно познакомились с тригонометрическими функциями — синусом, косинусом, тангенсом и котангенсом. И чётко уяснили себе следующее:. Синус, косинус, тангенс и котангенс — это просто какие-то безразмерные числа. Отношения сторон в прямоугольном треугольнике. Для каждого конкретного угла — свои. Тригонометрические функции крепко-накрепко связаны с углом.